Account volatility runs wild for most people during bear markets. This is not a pleasant experience for the average investor. Humans are creatures of routine and habit. It is in our nature to avoid volatile situations and return back to a safe, secure and steady state environment. But unfortunately for us, the investing game doesn’t reward those who can’t take on volatility. Instead of fearing and dreading volatility, we need to accept that it is part of the game and learn to cope with it. The strongest investors learn to actually embrace it.
We love this quote from Morgan Housel’s twitter feed:

The “price of admission” Morgan refers to is the psychological pain that comes with volatility. He’s talking about the difficulty of dealing with drawdowns and account swings. But if you can handle this volatility, you can usually earn higher returns, assuming a positive edge.
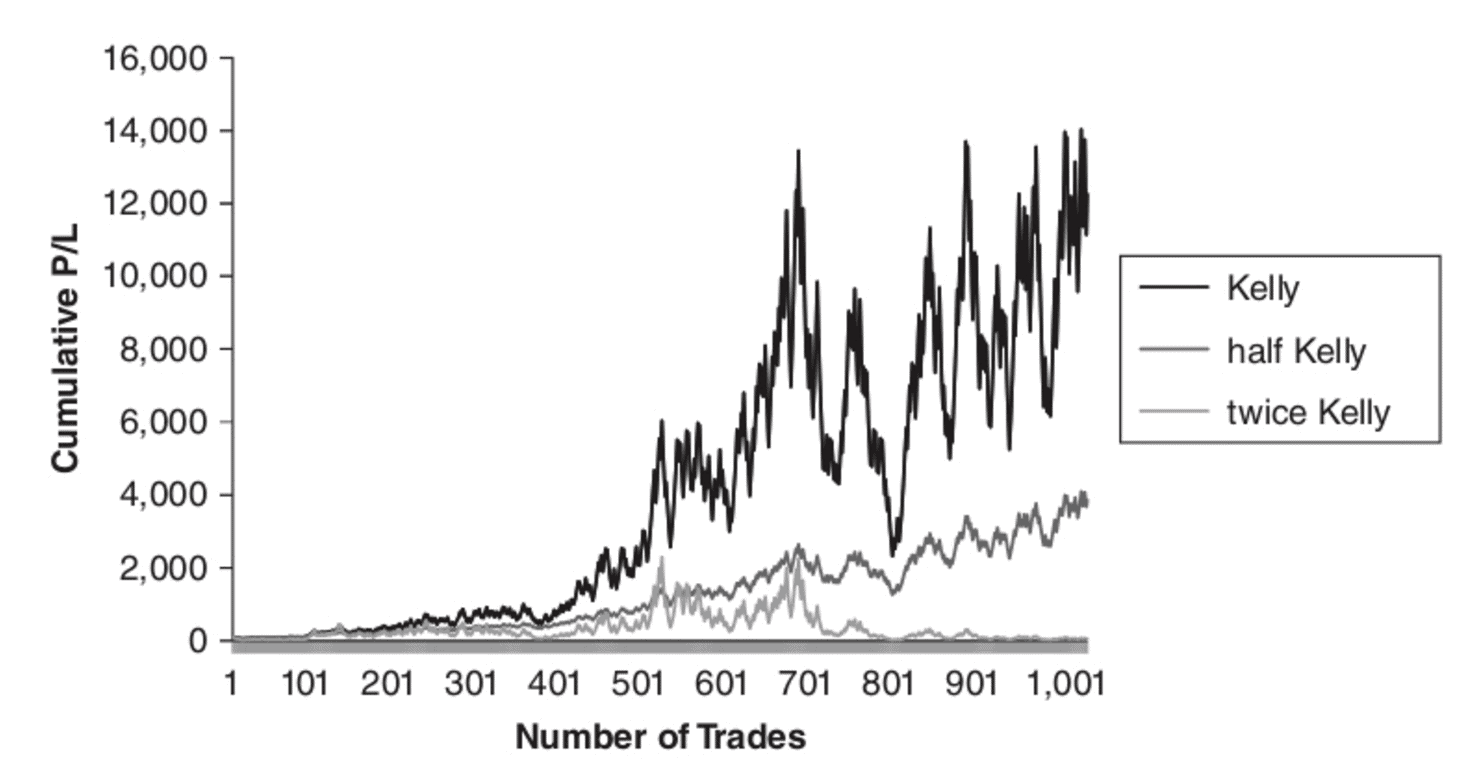
The graph below shows various Kelly bet systems. A Kelly bet is the optimal bet size an investor should place in order to achieve the largest return potential for a given investment strategy.
Source: Euan Sinclair Volatility Trading
It’s clear the Kelly bet is optimal in terms of returns. It makes far more money than making half a Kelly bet. But the “admission price” or volatility you have to endure with the full Kelly is MUCH higher than any other bet size. And few investors can stomach it. The fluctuations become impractical. Can you imagine waking up every day to watch your nest egg pop or drop by 7%?
We know that losing and volatility are painful. But we also know that the more volatility we endure, the more money we can make in the long run. This is of course assuming our investing process has positive edge.
So how can we pay the cheapest “price of admission” possible to suffer the least amount of pain, for the best long term outperformance possible?
Let’s start by addressing the volatility in losing investments.
Over the years we’ve found that the best way to help cope with downside volatility is to define it in advance. By defining losses, we cut out the negative emotions that tend to creep in with losing trades. Each of our trades has a set risk point where we exit for a small loss no matter what.
Using risk points in this manner makes defining losses in advance easy. We can calculate our total portfolio losses if every risk point were to hit simultaneously anytime we want. We can also see how this potential loss would change from adding or subtracting new and old positions. Comfort comes with this level of certainty.
This differs from standard stock picking or asset allocation because those approaches don’t define risk. They just keep track of how much their portfolio will likely fluctuate within a given year.
Now let’s look at the volatility that comes with winning investments.
With winners, it’s much easier to deal with volatility because you’re in the green. The fluctuations are all within the unrealized profit for your account. You don’t have to deal with thoughts of losing your base capital and going into the red. For this reason, we enjoy the volatility in our winners and hold on to them for as long as possible.
Refuse to accept downside volatility and embrace upside volatility. This is the formula we use to lower the “price of admission” in trading. We do this by setting risk points in advance, and letting our winners run. This is our coping mechanism.
How do you deal with the “price of admission” in your trading and investing process?
Bonus:
Can you solve this old floor trader’s riddle? They used to use it to assess mental speed for aspiring traders back in the old option pits. Email us for the right answer!
A pot contains 75 white beans and 150 black ones. Next to the pot is a large pile of black beans.
A somewhat demented cook removes the beans from the pot, one at a time, according to the following strange rule: He removes two beans from the pot at random. If at least one of the beans is black, he places it on the bean-pile and drops the other bean, no matter what color, back in the pot. If both beans are white, on the other hand, he discards both of them and removes one black bean from the pile and drops it in the pot.
At each turn of this procedure, the pot has one less bean in it. Eventually, just one bean is left in the pot. What color is it?